Quantum tomography

Quantum state tomography

Suppose somebody gives us a particle in an unknown quantum state and asks us to measure its wavefunction ψ(x). How can this be done? As we know from quantum mechanics, a single measurement, for example a measurement of the particle's position x, will produce a largely random result - and thus will tell us little about the particle's state. On the other hand, the state itself will be destroyed or significantly altered, so making further measurements on this particles is useless.

Thus in order to extract information about a quantum state we need many copies of it - a set of multiple particles prepared with the same wavefunction. But even that is not enough. Measuring many copies of the state with the same apparatus will only give us the probability density |ψ(x)|², but will tell us nothing about the wavefunction's phase, which is an equally important part of the quantum state characterization. In order to determine this phase, we need to also perform measurements in other bases. For example, if we also measure the probability density |ψ(p)|² in the momentum basis, we can tell much more about the quantum state than from the position probability density |ψ(x)|² alone.

Quantum tomography is the art of determining a quantum state from making measurements on multiple copies of the state with multiple modifications of the measurement apparatus. Because light is a quantum object, its quantum states can be measured by homodyne tomography, too. This is what we study in this project.

The primary approach we use in our work is homodyne tomography - the technique of characterizing a quantum state of light by means of multiple measurements of its electric field amplitudes at different quantum phases. This method allows complete characterization of the quantum state of an electromagnetic mode, in the form of either its density matrix or its Wigner function. It suits very well to our quantum state engineering effort because it tells us exactly which state we have constructed.

Quantum state tomography poses challenges of both fundamental and technical nature. We need to build fast, low-noise detectors that are able to amplify a subtraction charge that is equivalent to only about 10000 electrons within a bandwidth of a few hundred megahertz. Once this detector is set up, it produces a noisy, time-dependent trace that we see on an oscilloscope screen and can acquire with a computer. Then we need to reliably convert this trace into a set of quadrature values, determine the local oscillator phase associated with each of these values, and then apply a numerical algorithm to reconstruct the state. This reconstruction must be robust with respect to the noise, non-uniform distribution of the local oscillator phases, frequently insufficient number of data points. Once the state is reconstructed, we must be able to reliably estimate the error of this reconstruction.

Quantum process tomography

When we construct an electronic circuit, we base our design on precise knowledge of the properties of each component. All resistors, capacitors, transistors, and microchips come with a detailed specification sheet which describes how the electronic component will process different signals.

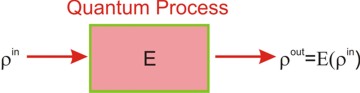The task of assembling a complex quantum circuit (for example, a quantum optical information processor) poses a similar requirement. We must have precise knowledge of the properties of each circuit component (be it, for example, a quantum memory cell, a noisy transmission line or a quantum computer gate): for each input quantum state we must be able to predict the output state after it has been processed by our device. This is a quantum version of the famous black box problem (for aesthetic reasons, the black box is shown in pink color in the figure on the right). Such a problem is approached through a procedure called quantum process tomography (QPT). The idea of QPT is to send a number of "probe" states into the black box and determine the output. Knowing the effect of the "black box" on the probe states, we can calculate its effect on any other state.

The basics of QPT are described in the tutorial. We have recently developed the continuous-variable version of QPT, i.e. characterization of processes on quantum states of light in certain spatiotemporal modes without making any a priori assumptions regarding the black box. Similarly to homodyne tomography, our technique has the advantage of complete characterization of the process over the entire optical Hilbert space. Its further advantage is that it is sufficient use coherent states of various amplitudes and shapes as the probe states. In other words, in order to find out what a quantum black box does to an adbitrary state of light, it is enough to measure what it does to simple laser pulses!

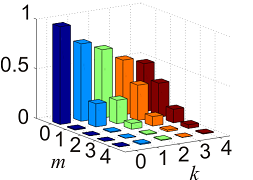Have a look at the picture on the right. This is the result of our experiment on quantum tomography of EIT-based optical memory. Columns of each color give the photon number distribution of the state retrieved from the memory given that the input is the k-photon state. For example, the dark blue columns indicate that if we store vacuum, the retrieved state is also, not surprisingly, almost exactly vacuum. The dark red columns, on the other hand, indicate the photon number distribution in the retrieved state if the input is the 4-photon state. Experimentally, it is very difficult to generate a pure 4-photon state to test what effect the storage will have on it. Yet we are able to obtain this information – and much more information that is essential for the understanding of the functionality of our memory cell – simply by storing and retrieving coherent states.

Additional work is underway, with the vision to make this method a universal standard for quantum device characterization. In particular, a robust algorithmic framework needs to be elaborated that would allow direct reconstruction of the superoperator from the experimental data acquired from the homodyne detector. Further open questions concern the evaluation of errors as well as the sampling frequency of the probe coherent states in the phase space.